| Durchführung: |
Theoretische Grundlagen:
Die wässrigen Lösungen der Triphenylmethanfarbstoffe
werden mit Laugen entfärbt:

Bild 1: Entfärbung von Kristallviolett
Die Geschwindigkeit der Reaktion ist von der Konzentration des
Kristallvioletts cKV und der Hydroxidionen
cOH abhängig (Reaktion 2. Ordnung).
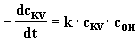 |
(1) |
Ist die Konzentration der OH--Ionen wesentlich
größer als die des Kristallvioletts, ändert sich
diese während der Reaktion kaum. Sie bleibt nahezu konstant
und ihr Einfluß auf die Reaktionsgeschwindigkeit kann mit Hilfe
einer Proportionalitätskonstante berücksichtigt werden:
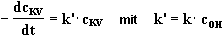 |
(2) |
Unter diesen Bedingungen liegt eine Reaktion pseudo-erster Ordnung vor.
Berechnung der Geschwindigkeitskonstante k’
Durch Integration der Gleichung (2) erhält man:
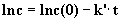 |
(3) |
Die Kombination der Gleichung (3) mit dem Lambert-Beerschen Gesetz
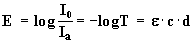 |
(4) |
E = Extinktion, Ε = molarer dekadischer Extinktionskoeffizient,
Ia = Intensität des austretenden Lichts, I0 = Intensität des eintretenden Lichts,
c = Konzentration der Lösung, d = Dicke der durchstrahlten Lösungsschicht.
liefert einen Zusammenhang von k’ und c:
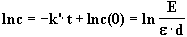 |
(5) |
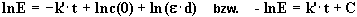 |
(6) |
Die Geschwindigkeitskonstante k ergibt sich aus Gleichung (2):
Grafische Ermittlung der Aktivierungsparameter
Die Arrhenius-Gleichung in ihrer logarithmierten Form lautet:
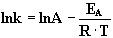 |
(8) |
k = Geschwindigkeitskonstante, A = Häufigkeitsfaktor, T = absolute Temperatur [Kelvin]
EA = Aktivierungsenergie [kJ·mol-1], R = allgemeine Gaskonstante (8.3144 J·K-1·mol-1)
Die Auftragung von lnk gegen 1/T ergibt eine eine Gerade mit
der Steigung m1, aus der sich die Aktivierungsenergie
EA berechnen läßt:
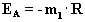 |
(9) |
Der Achsenabschnitt y(x=0) gibt den Wert für lnA an.
Eyring-Gleichung:
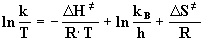 |
(10) |
DH¹ = Aktivierungsenthalpie [kJ·mol-1],
kB = Boltzmannkonstante (1.381·10-23 J·K-1),
h = Planksche Konstante (6.626·10-34 J·s)
Die Auftragung von ln(k/T) gegen 1/T liefert eine Gerade, aus
deren Steigung m2 sich die Aktivierungsenthalpie
DH¹
berechnen läßt:
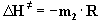 |
(11) |
Mit Hilfe des Achsenschnitts
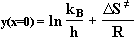 |
(12) |
wird DS¹
ermittelt und somit die Berechnung von
DG¹
für die entsprechende Reaktionstemperatur ermöglicht.
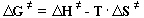 |
(13) |
dG¹ =
Freie Aktivierungsenthalpie zur Bildung des aktivierten Komplexes
DS¹ =
Aktivierungsentropie [Entropieeinheiten]
 | kleine Werte für EA und DH¹
Þ rasche Reaktion |
 | große Werte für EA und DH¹
Þ langsame Reaktion |
 | lnA klein entsprechend DS¹
stark negative Werte Þ langsame Reaktion |
 | lnA groß entsprechend DS¹
schwach bis stark positive Werte Þ rasche Reaktion |
|
Versuchsaufbau:

|
-
In eine Küvette werden 2 mL einer
5·10-5 molaren Triphenylmethanfarbstoff-Lösung
pipettiert. In eine zweite Küvette gibt man 2 mL der 0.1
molaren Natronlauge.
-
Die beiden Küvetten werden
anschließend mit Stativklammern in einem temperierten
Wasserbad gehaltert, in das ein Kontaktthermometer und ein
Thermometer mit 1/10 °C-Einteilung eintaucht.
Folgende Temperaturbereiche empfehlen sich: für die
Entfärbung von Kristallviolett 39 - 49 °C, von Fuchsin
20 - 26 °C und von Malachitgrün 17 - 25 °C.
An Stelle des Kontaktthermometers können Sie auch die
Steuerungsfunktion
der Chembox nutzen.
-
Schreiberausgang des Photometers wird an
Eingang 1 der Chembox angeschlossen.
-
Sicherstellen, daß die Chembox mit dem
Computer verbunden ist. Computer und Photometer einschalten.
|
-
Während des Temperaturangleichs zwischen
dem Wasserbad und den Reaktionslösungen erfolgt die Justierung
des Photometers: mit dem Wellenlängenknopf stellt man das
Absorptionsmaximum des entsprechenden Triphenylmethanfarbstoffes ein
(für Fuchsin 545 nm, für Kristallviolett 590 nm, für
Malachitgrün 615 nm). Nach erfolgtem Nullabgleich bringt man
eine Küvette in den Strahlengang, in der man zu 2 mL der
Triphenylmethanfarbstoff-Lösung 2 mL Natronlauge pipettierte.
Sobald das Transmissionsmaximum erreicht ist, wird es auf die
Transmission T = 100 % abgeglichen.
-
Kalibrierung der Chembox:
über den Menüpunkt Optionen - Kalibrierung
ist zunächst der Kalibrierdialog für den entsprechenden
Eingang an der Chembox zu aktivieren. In die Textfelder hinter
Ref1 bzw. Ref2 trägt man zwei Eichwerte ein: bei
Ref1 0.0 V und bei Ref2 1.0. Die Küvette wird
aus dem Küvettenschacht genommen und Button Set hinter
Ref1 geclickt. Nach Einsetzen der entfärbten
Reaktionslösung clickt man Set hinter Ref2. Die
beiden Buttons Set müssen mit einem grünen Haken
versehen sein. Manchmal erscheint beim Clicken dieses Häkchen
nicht. In solchen Fällen ist es ratsam, den Kalibriervorgang
erneut durchzuführen.
Sind alle Schritte korrekt ausgeführt worden, stellt sich
das Dialogfeld wie folgt dar:
 Mit der Formel rechnet Chemex den Wert der Spannung am
Chembox-Eingang für Spannung1 (V1) in die Spannung nach
Kalibrierung (K1) um.
Mit der Formel rechnet Chemex den Wert der Spannung am
Chembox-Eingang für Spannung1 (V1) in die Spannung nach
Kalibrierung (K1) um.
-
Einstellen - Kanäle definieren
Die Karteikarte Messen/Einstellen soll folgendes Bild haben:

Mit K1 wird das kalibrierte Signal des Photometers bezeichnet.
K1 · 100 steht für die
Transmission T. Der blaue Kanal
verwendet ebenfalls das Signal K1, rechnet dieses jedoch über
die Formel 2 - log (K1 · 100)
in den Wert für die Extinktion E
um. Auf dem Meßbildschirm wird sowohl die Kurve für die
Transmission als auch für die Extinktion dargestellt.
Aufnahme der Absorptionsspektren:
-
Versuch-Symbol
oder entsprechende
CHX-Datei
anclicken.
-
Nach einem 15 minütigen Temperaturangleich
wird die Reaktionstemperatur auf 1/10 °C notiert.
-
Die Natronlauge zügig zu der Lösung
des Triphenylmethanfarbstoffs gießen, die Küvette kurz
schütteln, in den Strahlengang des Photometers bringen und
die Messung durch einen Click auf den 1/0-Knopf starten.
-
Wenn sich die Extinktion (spätestens nach
2 Minuten) nicht mehr ändert, 1/0-Knopf wieder anclicken.
-
Kurve unter einem Namen
im gewünschten Arbeitsbereich
abspeichern.
-
Kurve beschriften, z.B. mit den Reaktanden, evtl. dazu
Name des Experimentators.
-
Wieder abspeichern.
Auswertung
der bei der Entfärbung von Malachitgrün mit der Chembox
erfaßten Extinktionswerte in Microsoft Excel - Ermittlung
der Geschwindigkeitskonstanten k
Excel, die universell einsetzbare Tabellenkalkulation von Microsoft,
kann größere Datenmengen auf einmal bewältigen, auf vielerlei Arten
umrechnen und schließlich grafisch darstellen. Mit etwas Übung
lassen sich daher relativ schnell optisch ansprechende und
aussagekräftige Tabellen und Diagramme erstellen.

 | Die durch Aktivierung der Tabellenfunktion in Chemex
(Karte Schreiber - Werte-Tabelle) generierten Meßwerte
werden im Menü der Wertetabelle Datei - Tabelle exportieren
abgespeichert. Der Dateityp sollte bei *.txt belassen werden, da
dieses Format beim Importieren in Excel die geringsten Probleme bereitet.
Nach dem Öffnen der Datei und Betätigung aller folgenden Dialoge ist
die gesamte Tabelle in Excel übernommen. Beim Importieren weiterer
Tabellen legt Excel für jede Meßreihe eine neue Arbeitsmappe an. Durch
Verschieben der Tabellenblätter lassen sich die einzelnen Meßreihen
in einer Mappe zusammenfassen. Dies erfolgt mit dem Menübefehl
Bearbeiten - Blatt verschieben / kopieren. Es ist
immer die gleiche Zielmappe zu wählen. Die ersten drei Zellen
sollen unberücksichtigt bleiben, so daß sie für diverse
Eintragungen zur Verfügung stehen. |
 | Aus den in Excel importierten Extinktionswerten
E sind entsprechend Gleichung (6) -lnE - Werte zu berechnen. Hierzu
wird in diejenige Zeile, die den ersten -lnE-Wert erhalten soll
= -LN(B4) geschrieben, wenn B4 der erste Extinktionswert ist.
Es erscheint der Wert, der aufgrund der eingebenen Formel errechnet wird.
Indem die Zelle an ihrem Knoten (rechtes unteres Eck) in der Datenreihe
nach unten gezogen wird, kann die Formel in alle Zellen der Datenreihe
kopiert werden. Analog wird mit den anderen Meßreihen verfahren. | In Diagrammen werden jeweils die Auftragungen von E
gegen t und -lnE gegen t realisiert (Bild 6, 7): Von der obersten Zelle
an ist der gesamte Bereich der darzustellenden Meßwerte aller Meßreihen
einschließlich der Werte für t zu markieren. Für die Auftragung von -lnE
gegen t muß die Markierung der entsprechenden Werte unter Betätigung
von Strg erfolgen. Anschließend wird Excel mit dem Menüpunkt
Einfügen - Diagramm - Als neues Blatt angewiesen,
eine Grafik mit markierten Zellen zu erstellen. Man wählt ein Punkt
(XY)-Diagramm mit Gitternetzlinien. Im Schritt 4 der Grafikerstellung
weist man Excel an, eine 1 Spalte als x-Werte und 2 oder 3 Zeilen als
Legendentext (siehe Gestaltung der Spaltenköpfe im Tabellenblatt) zu
verwenden. Im nächsten Schritt erfolgt die Belegung der Achsen. Auf
die Legende kann verzichtet werden.
Im nun generierten Diagramm kann durch Doppelclick auf eine Datenreihe
deren Gestaltung den Bedürfnissen (z.B. Farbe und Form der Meßpunkte,
Darstellung als Linie) angepaßt werden. Nach Doppelclick auf die
Fläche läßt sich die Zeichnungsfläche formatieren, z.B. der beim
Ausdruck störende graue Hintergrund entfernen. Doppelclick auf die
Achsen eröffnet die Möglichkeit, deren Skalierung zu ändern. |
 | Bis zu einem Reaktionsumsatz von ca 80 % werden
anschließend die -lnE - Werte in neue Spalten eingefügt. Durch
Aktivierung des Funktionsassistenten fx
kann mit der Funktion RGP unter der Gruppe Statistik
mittels linearer Regression die Steigung von Wertepaaren und damit
im vorliegenden Fall die Konstante k’ errechnet werden. Der
Funktionsassistent verlangt nach y-Werten. Nachdem in der
entsprechenden Spalte die zu berücksichtigenden lnE - Werte
markiert sind, erscheint im Textfeld der y-Werte nun ein Eintrag
z.B. J4;J28, falls J die aktuelle Spalte ist. Per Tastatur trägt
man in das Feld für die x-Werte A4;A28 ein. Damit wird das Programm
darauf hingewiesen, die Zeitwerte, die ja in Spalte A stehen sollen,
als die zu den lnE - Werten gehörigen x-Werte zu verwenden. Der
Dialog ist mit Ende abzubrechen. In der gewählten Zelle
taucht nun der Wert für die Steigung des linearen Bereichs auf.
Nachdem diese Schritte für die übrigen Messungen der Versuchsreihe
wiederholt sind, sollten die ermittelten Werte auf eine
vernünftige Anzahl an Nachkommastellen gebracht werden.
|
| Die nackten Zahlenwerte der errechneten Steigungen verlangen nach
grafischer Untermauerung. Die momentane Darstellung der Auftragung
von -lnE gegen t erfüllt diese Zweck unzureichend. Nötig ist die
Hervorhebung des gewählten linearen Bereichs durch das Einzeichnen
einer Ausgleichsgerade, die nur die relevanten Meßpunkt
berücksichtigt (Bild 7). Zwar bietet Excel die Möglichkeit,
eine Trendlinie zu jeder Datenreihe einzufügen. Allerdings
erstreckt sich diese Ausgleichsgerade über die gesamte Datenreihe,
also u. U. auch über eine flach verlaufende Induktionsphase oder
über einen Bereich, in dem die Reaktion schon so gut wie beendet
ist. Ein kleiner Kunstgriff hilft diesen Mangel zu umgehen:
 | Die bis zu einem Reaktionsumsatz von ca 80 %
in eine neue Spalte eingefügten -lnE - Werte und die
entsprechenden Zeitwerte einer Datenreihe werden unter
Betätigung der Strg - Taste synchron markiert. Nach dem
Kopieren der Markierungen wechselt man zum Diagramm der
Auftragung von -lnE gegen t und wählt dort den Menüpunkt
Bearbeiten - Inhalte einfügen. Excel wird
mitgeteilt, daß die kopierten Zellen als Neue Datenreihe
eingefügt werden sollen, die Werte (Y) aus Spalten
stammen und die Rubriken (X - Achsenwerte) in erster Spalte
stehen. |
 | Nach Click mit der rechten Maustaste auf
die neue Meßpunktreihe ist Trendlinie einfügen zu wählen
und der sich öffnende Dialog zu bestätigen. Durch Click mit
der linken Maustaste auf die Ausgleichsgerade läßt sich diese
unter Optionen - Trend nach vorne oder hinten
verlängern und unter Optionen - Formel eingeben
die Geradengleichung ermitteln. Der Koeffizient vor x gibt
den Wert für k’ an (Bild 7). |
Obige Schritte sind bei den übrigen Datenreihen zu wiederholen. Ergebnis etwa:

Bild 5: Darstellung der Meßwerte in Excel (1: 17 °C, 2: 21.1 °C, 3: 25 °C)

Bild 6: Extinktion (1: 17 °C, 2: 21.1 °C, 3: 25 °C)

Bild 7: Ermittlung der Proportionalitätskonstanten k'
| Messung |
T [°C] |
T [K] |
k’ [l·mol-1·s-1] |
k [l·mol-1·s-1] |
| 1 |
17 |
290.15 |
0.0448 |
0.896 |
| 2 |
21.1 |
294.25 |
0.0599 |
1.198 |
| 3 |
25 |
298.15 |
0.0811 |
1.623 |
Tabelle 1: Geschwindigkeitskonstante k (gemäß Reaktionsansatz u. Gleichung (2): k = k’ / 0.05)
Ermittlung der Aktivierungsparameter
Auftragung von lnk und ln(k/T) gegen 1/T in Microsoft Excel

Tabelle 2: Berechnung der Aktivierungsparameter

Bild 8: Auftragung nach ARRHENIUS (1) und EYRING (2)
Reaktivität der Triphenylmethanfarbstoffe im Vergleich
Unter den beschriebenen Bedingungen
werden auch Fuchsin und Kristallviolett mit Natronlauge
umgesetzt und die Aktivierungsparameter bestimmt.
| Aktivierungsparameter |
Malachitgrün |
Fuchsin |
Kristallviolett |
| EA [kJ·mol-1] |
53.3 |
53.7 |
57.6 |
| lnA |
21.98 |
21.86 |
21.39 |
| DH¹ [kJ·mol-1] |
50.9 |
51.2 |
54.9 |
| DS¹ |
-70 |
-71 |
-76 |
| DG¹ [kJ·mol-1] bei 298.15 [K] |
71.8 |
72.4 |
77.5 |
Tabelle 3: Aktivierungsparameter im Vergleich
Deutung des Versuchsergebnisses:

Bild 9: Kristallviolett (1), Fuchsin (2), Malachitgrün (3)
Durch Reaktion des zentralen C-Atoms mit dem Nucleophil OH-
wird das verzweigte chromophore Tritylsystem unterbrochen.
Die unterschiedliche Reaktivität der Triphenylmethanfarbstoffe
(Kristallviolett <<
Fuchsin < Malachitgrün)
beruht auf den unterschiedlichen Subsituenten. Im Kristallviolett
wird die Elektronendichte am zentralen C-Atom durch den +M-Effekt
von zwei Dimethylamino-Gruppen stark erhöht, so daß der
Angriff des Nucleophils erschwert ist. Im Malachitgrün liegt
nur eine nicht blockierte Dimethylamino-Gruppe vor, wodurch die
Reaktion mit dem Nucleophil erleichert wird. Die im Vergleich zum
Malachitgrün etwas geringere Reaktivität des Fuchsins
ist auf zwei Amino-Gruppen (+M-Effekt) und die Methyl-Gruppe
(+I-Effekt) im Ring II zurückzuführen, die die
Elektronendichte am zentralen C-Atom erhöhen (Bild 9).
Anmerkungen:
 | Eine Messung der Reaktionsgeschwindigkeit in situ anhand einer
kontinuierlichen Registrierung photometrisch erfasster Meßdaten
ist nur dann möglich, wenn rasch ablaufende Reaktionen vorliegen
(siehe geforderte Temperaturkonstanz). |
 | Bei der Auswertung einer Reaktion erster Ordnung sind die
Meßdaten relevant, die bis zu einem Reaktionsumsatz von
mindestens 70 % registriert werden. Bei Reaktionen zweiter Ordnung
mit äquivalenten Ausgangskonzentrationen ist ein
Reaktionsumsatz von mindestens 50 % zu berücksichtigen. |
 | Um verläßliche kinetische Daten zu erhalten, ist
es notwendig, die Umsetzung bei mindestens drei verschiedenen
Reaktionstemperaturen durchzuführen. Die Meßpunkte in
den Auftragungen lnk bzw. ln(k/T) gegen 1/T sollen möglichst
auf einer Geraden liegen (Bild 8). Zeigen sie eine
größere Streuung, so wird zwar durch Ausgleichsrechnung
eine optimale Gerade ermittelt - die vollzogene Ausgleichsrechnung
erhöht jedoch die Genauigkeit der Ergebnisse in keiner Weise.
Bei der Angabe von Fehlergrenzen ist große Kritik angebracht.
Wenn drei Meßpunkte im Diagramm lnk bzw. ln(k/T) gegen 1/T
nicht auf einer Geraden liegen, wird die Geschwindigkeitskonstante
k bei einer vierten Reaktionstemperatur gemessen, da jeder
Meßpunkt der "Ausreißer" sein kann. Grundsätzlich
empfiehlt es sich, durch Verbesserung der Meßmethode (siehe
auch exakt thermostatisierte Reaktionslösungen) die Genauigkeit
der Meßwerte zu erhöhen. |
 | Obwohl die rechnerische Auswertung der Aktivierungsparameter
exakt ausgeführt werden soll, darf sie nicht eine zu große
Genauigkeit vortäuschen. Aktivierungsenergie und Aktivierungsenthalpie
werden in Veröffentlichungen auf eine Kommastelle angegeben. Die
Aktivierungsentropie soll grundsätzlich in ganzen Einheiten
aufgeführt werden. Bei Entropien D
S¹ <± 10 darf eine
Dezimale angegeben werden. Bei der Angabe der lnA-Werte sind 2 Dezimalen
statthaft. |
|