Lösung:
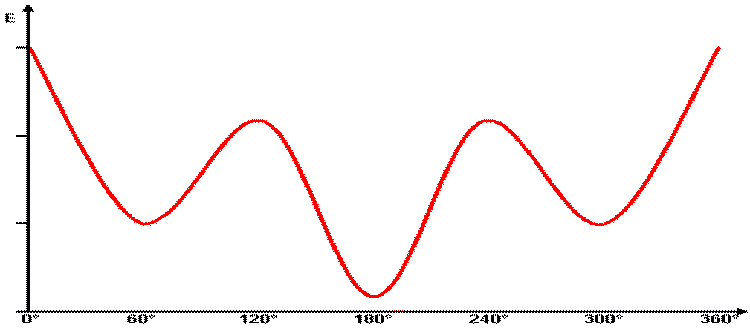
Sieht Ihr Graph auch so aus? Er zeigt die Energie im Butanmolekül bei der Rotation um die C2-C3-Bindung an.

0°	60°	120°	180°	240°	300°	360°=0°
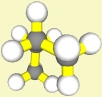
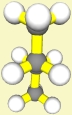
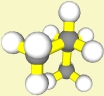
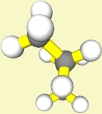
(voll)ekliptisch	(schief-)gestaffelt	(partiell)ekliptisch	gestaffelt	(partiell)ekliptisch	(schief-)gestaffelt	(voll)ekliptisch
	(gauche)		(anti)		(gauche)
Maximum	Zwischen-minimum	Zwischen-maximum	Minimum	Zwischen-maximum	Zwischen-minimum	Maximum

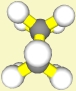
• Beim Torsionswinkel 0° findet man 1 absolutes Maximum bei ekliptischer Konformation.

• Bei den Torsionswinkeln 60° und 300° findet man insgesamt 2 Zwischenminima: gestaffelte Konformationen; um diese von der bei 180° zu unterscheiden, nennt man sie "gauche".

• Bei den Torsionswinkeln 120° und 240° findet man insgesamt 2 Zwischenmaxima: ekliptische Konformere.

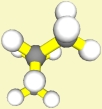
• Beim Torsionswinkel 180° findet man 1 absolutes Minimum bei günstigster gestaffelter Konformation; um diese von der bei 60 und 300° zu unterscheiden, nennt man sie "anti".

Nun können wir die Frage nach der Amplitude beantworten: Die Größe (Sperrigkeit) der Reste der an der Rotation um die C-C-Bindung beteiligten C-Atome ist ausschlaggebend. Bei Ethan sind es lauter gleiche, kleine H-Atome, bei Butan kommt eine größere Methylgruppe vor; dadurch ist auch die abstoßende Wirkung größer.

Die Größe der Methylgruppen behindert die Rotation um die C2-C3-Bindung. Das bezeichnet man allgemein als Rotationsbarriere. Die Höhe dieser Barriere ist ein Energiemaß und wird in kJ/mol angegeben.