Chiralitätsisomerie
Überlegen Sie
nochmal:
Das Inversionszentrum befindet sich an dem
grün markierten Punkt I.
Dies bedeutet, dass nun keine Ebene mehr vorliegt, sondern über einen Punkt gespiegelt werden kann. Wenn Sie noch einmal an das Beispiel mit dem Schmetterling denken, so ist es hier ähnlich. Man kann irgend einen Punkt auf dem Objekt nehmen, denkt sich eine Gerade von dem Punkt durch das Inversionszentrum und legt jenseits des Zentrums den gespiegelten Punkt im gleichen Abstand auf der Geraden ab.
Dies bedeutet, dass nun keine Ebene mehr vorliegt, sondern über einen Punkt gespiegelt werden kann. Wenn Sie noch einmal an das Beispiel mit dem Schmetterling denken, so ist es hier ähnlich. Man kann irgend einen Punkt auf dem Objekt nehmen, denkt sich eine Gerade von dem Punkt durch das Inversionszentrum und legt jenseits des Zentrums den gespiegelten Punkt im gleichen Abstand auf der Geraden ab.
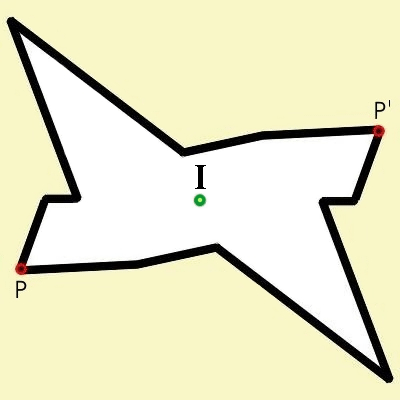
Wenn man nun eine Gerade durch die Punkte P und I legt, so kommt man mit dem gleichen Abstand wie zwischen P
und I zum Punkt P'.
Probieren Sie es gleich einmal selbst aus! Legen Sie ein Geodreieck mit der 0-Markierung an Punkt
I auf den Monitor und Sie
werden sehen, dass es z.B. für jeden schwarzen Randpunkt auf der anderen Seite in gleicher Entfernung eine Entsprechung gibt.
In den meisten Fällen ist das Inversionszentrum auch gleichzeitig der Schwerpunkt eines Objektes.